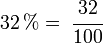ALUMNOS DE LAE. 402

BIENVENIDOS A AL BLOG DE MATEMÁTICAS FINANCIERAS.

Objetivos del curso.

  

·  Desarrollará métodos matemáticos propios de la administración que impulsen a ésta a lograr la maximización de sus recursos financieros. Determinar el valor de: monto,  intereses, descuentos, pagos etc. Mediante las fórmulas correspondientes de interés simple y compuesto.
·    Identificará las diferencias entre los tipos de anualidades más comunes y determinara el valor de los parámetros característicos de estas, como: monto renta, valor presente, plazo etc.
·     determinará el valor del los parámetros característicos de una amortización y de      un fondo de amortización, además de representarlos en forma tabular.

Concepto de Matemáticas financieras

La matemática financiera es una rama de la matemática aplicada que se ocupa de los mercados financieros.

Se analizará en valor de capital en  el tiempo.

 TEMARIO DE LA MATERIA DE MATEMÁTICAS FINANCIERAS

  

1. Conceptos Básicos

1.1 Tanto por ciento:

En matemáticas, un porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador. También se le llama comúnmente tanto por ciento, donde por ciento significa “de cada cien unidades”. Se usa para definir relaciones entre dos cantidades, de forma que el tanto por ciento de una cantidad, donde tanto es un número, se refiere a la parte proporcional a ese número de unidades de cada cien de esa cantidad.

El porcentaje se denota utilizando el símbolo %, que matemáticamente equivale al factor 0,01 y que se debe escribir después del número al que se refiere, dejando un espacio de separación.¹ Por ejemplo, "treinta y dos por ciento" se representa mediante 32 % y significa 'treinta y dos de cada cien'. También puede ser representado como:

y, operando:

El 32 % de 2000, significa la parte proporcional a 32 unidades de cada 100 de esas 2000, es decir:

640 unidades en total.

1.2 Aplicaciones del tanto por ciento

El porcentaje o tanto por ciento (%), es una de las aplicaciones más usadas de las proporciones o razones .

El porcentaje es una forma de comparar cantidades, es una unidad de referencia que relaciona una magnitud (una cifra o cantidad) con el todo que le corresponde (el todo es siempre el 100) , considerando como unidad la centésima parte del todo.

Ejemplos:

1 centésimo  = 

5 centésimos = 

50 centésimos = 

Nota importante. No olvidar que las fracciones deben expresarse siempre lo más pequeñas posible, deben ser fracciones irreductibles.

¿Qué significa 50 %?: Significa que de una cantidad que se ha dividido en cien partes se han tomado 50 de ellas, o sea, la mitad.

¿Qué significa 25 %?: Significa que de un total de 100 partes se han tomado 25, o sea ¼ ( 25/100 al simplificar por 5, se reduce a  ¼).

Cálculo de Porcentaje

El Porcentaje o Tanto por ciento se calcula a partir de variables directamente proporcionales (significa que si una variable aumenta la otra también aumenta y viceversa).

En el cálculo intervienen cuatro componentes:

Cantidad Total             ----             100 % 
Cantidad Parcial           ----            Porcentaje Parcial

Ejemplo

(Cantidad total)       $ 1.000  -   equivale al   -     100 % (porcentaje total) 
(Cantidad parcial)    $  500    -   equivale al   -      50  %  (porcentaje parcial)

Existen tres situaciones o tipos de problemas que pueden plantearse. Éstos son :

1.- Dada una cantidad total, calcular el número que corresponde a ese porcentaje (%) parcial :

Ejemplo: ¿Cuál (cuanto) es el 20% de 80?

	Cantidad	Porcentaje
Total	80	100
Parcial	x	20

Para resolverlo, se hace:

Resolvemos la incógnita  (x):

Haciendo la operación, queda:

Simplificando, queda:

Respuesta: el 20 % de 80 es 16.

2.- Calcular el total, dada una cantidad que corresponde a un porcentaje de él .

Ejemplo: Si el 20 % de una cierta cantidad total es 120 ¿Cuál es el total?

Cantidad	Porcentaje
x	100
120	20

Para resolverlo, se hace:

Resolvemos la incógnita  (x):

Haciendo la operación, queda:

Simplificando, queda:

Respuesta: 120 es el 20 % de un total de 600.

3.- Dado el total y una parte de él calcular que % es esa parte del total .

Ejemplo:  ¿ Qué porcentaje es 40 de 120?

Cantidad	Porcentaje
120	100
40	x

Para resolverlo, se hace:

Resolvemos la incógnita  (x):

Haciendo la operación, queda:

Simplificando y haciendo la división, queda:

Respuesta: 40 es el 33,33 % de 120.

\

1.3 Problemas de porcentaje

Ejercicios para  realizar en clase

Actividades en clase

1.4 Progresiones aritméticas

1.5 Cálculo de logaritmos

  2. Interés Simple

2.1 Introducción

2.2 Valor  presente y futuro

2.3 Interés, tasa de interés y tipo de interés

2.4 Descuento

2.5 Gráficas de interés simple

2.6 Ecuaciones equivalentes

3. Interés Compuesto

3.1 Introducción

3.2 Valor presente y futuro

3.3 Tasa nominal, efectiva y equivalente

3.4 Tiempo

3.5 Tasa de interés

3.6 Ecuaciones equivalentes

4. Anualidades

4.1Tipos de anualidades

4.2 Anualidades simples

4.3 Anualidades anticipadas

4.4 Anualidades diferidas

           4.5 Anualidades generales5. Amortización

5.1 Introducción

5.2 Tasa de interés en una amortización

5.3 Depósitos a un fondo de amortización

5.4 Tasa de interés en un fondo de amortización.

6. Depreciación

5.1 Concepto de depreciación

5.2 Método de línea recta

5.3 Método de porcentaje fijo

  

 FORMA DE EVALUAR EN CADA PARCIAL

Examen	40%
Ejercicios en clase	30%
Exposición	20%
Participación	10%
total	100%

Díaz, Mata Alfredo (2005)  Matemáticas Financieras    Mc Graw Hill

Ayres, Frank Jr.     (2006)  Matemáticas Financieras    Mc Graw Hill

Licoyán Portus G.  (2006)  Matemáticas financieras     Mc Graw Hill